Arrieros somos…

… y en el camino nos encontraremos.

En el último anuncio constatamos que casos como el de los dos jefes de proyecto y la UTE –del tipo dilema del prisionero- ponen en jaque nuestra concepción de racionalidad. No hay mejor forma de resumir el conflicto del dilema que recordar lo que una vez dijo Oscar Wilde: “puedo resistirme a cualquier cosa menos a la tentación”. No cabe duda que la tentación alcanza su punto álgido cuando ambos oponentes piensan que sólo se enfrentarán al dilema una vez un sus vidas. Pero, ¿qué ocurre si nos volvemos a encontrar ante un dilema similar, no una ni dos, sino varias veces. Después de todo, el mundo de los negocios, y el de los proyectos en particular, es un escenario de caminos que se entrecruzan a lo largo del tiempo. Si sé que solamente me enfrentaré al otro jefe de proyecto una vez en la vida, aún puedo valerme de su ingenuidad para desertar, esperando que el coopere, para llevarme el máximo beneficio. Pero si nos volvemos a encontrar, ¿cómo actuará esta vez? ¿Entraremos en una escalada de destrucción mutua?

Para averiguarlo, Robert Axelrod pidió a varios especialistas en teoría de juegos, economistas, sociólogos, politólogos y psicólogos que aportaran estrategias para simular por ordenador un dilema iterativo del prisionero; como por ejemplo cooperar siempre, cooperar y desertar alternativamente, cooperar o desertar según el resultado de lanzar una moneda al aire, etc. Todas las estrategias se enfrentaban dos a dos e iban acumulando el número de puntos obtenidos en cada lance. La estrategia ganadora fue una muy sencilla denominada “donde las dan las toman”. Era una estrategia que ocupaba cuatro líneas de código y que venía a decir coopera la primera vez y luego haz lo que haya realizado el oponente en la partida anterior. El lector puede encontrar un simulador en el siguiente sitio, hay que seleccionar un par o más de estrategias (tit_for_tat es la donde las dan las toman) e indicar el número de rondas. Notar que puede haber algunos enfrentamientos en los que no se la ganadora, aunque sí en el cómputo total. En el blog de Mario López de Ávila podemos encontrar un ejemplo muy interesante del valor de esta estrategia en su comentario del libro “la estrategia de los delfines”. Ver el dilema iterativo del prisionero como una pauta de comportamiento podría ofrecer una luz sobre por qué, a pesar de los pesares, la cooperación sigue presente independientemente de significado ético que podamos atribuirle. Imaginemos que ahora sometemos a una selección artificial a las estrategias que no han superado como otras cierto umbral de puntuación en momentos dados, ¿qué estrategia tiene más probabilidades de llegar al final? Obviamente, la naturaleza no cuenta solamente con un mecanismo de selección, sino con mutaciones al azar que en nuestro juego iterativo equivaldría a la aparición de nuevas estrategias no necesariamente cooperativas. Y aquí es donde entramos en el siguiente paso.

Aún así, se puede llegar a una situación de equilibrio como describió el biólogo evolutivo John Maynard Smith en su dilema del los halcones y las palomas. Imaginemos una población en la que solamente convive una especie con sólo dos tipos de comportamiento, que llamaremos halcón y paloma. Si un halcón encuentra comida y está presente otro miembro de la especie, luchará por conseguirlo. En cambio, si es una paloma la que encuentra comida estando presente otro miembro de la especie, nunca iniciará una lucha, huyendo si la atacan y amenazando si no. Consideremos que el valor del alimento es de 50 puntos. Si no se consigue el alimento después de haber atacado se es herido y se pierden 100 puntos. Finalmente, por un acto de amenaza se pierden 10 puntos, independientemente de si se consigue o no el alimento. Con todo esto podemos construir la tabla de resultados. Cuando un halcón se enfrenta a otro halcón, los dos atacan, uno se lleva el alimento y gana 50 puntos, y el otro resulta herido y pierde 100 puntos; el resultado medio para el halcón en este tipo de enfrentamientos es pues de -25 puntos. Cuando un halcón se enfrenta a una paloma, ésta huye quedándose con 0 puntos mientras que el halcón consigue los 50 puntos. Finalmente, cuando una paloma se enfrenta a una paloma, las dos amenazan, una se lleva el alimento y gana 40 puntos, y la otra no y pierde 10 puntos. El resultado medio para la paloma en este tipo de enfrentamientos es pues de 15 puntos -40 menos 10 dividido por 2. La tabla es la siguiente:


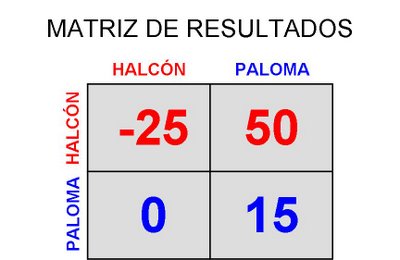
Con una población inicial de palomas, todo el mundo consigue por término medio 15 puntos. Nadie resulta herido y todos consiguen alimento. Imaginemos que se produce una mutación y surge un halcón, conseguirá siempre alimento (50 puntos) sin coste alguno. Con una poco población de halcones, su ventaja les hará prosperar teniendo descendientes su comportamiento de halcón. Pero si llegan a ser numerosos habrá mas enfrentamientos entre halcones, perdiendo de media 25 puntos disminuyendo así su población. La paloma se las arreglará otra vez bien, volviendo a aumentar su población y volviendo al punto de partida. Como se ve, los extremos no son estables habiendo una evolución hacia un término medio. Esto es lo que se conoce en teoría de juegos como equilibrio mixto o de Nash, hallazgo que, entre otras cosas le valió el premio Nobel de economía de 1994. En este sitio se puede jugar al juego de los halcones y las palomas, cambiando el sistema de puntuación, y comprobar cual es el punto de equilibrio. Para la tabla que hemos considerado arriba, la misma que la que hay por defecto en la simulación, se obtiene que el punto de equilibrio se alcanza para una población de halcones del 58,3% o, lo que es lo mismo, cuando en la población hay cinco palomas por cada siete halcones -¿será nuestro mundo así?...

¿Es compatible esto con la metáfora de los delfines? Resulta que el resultado es el mismo que si cada miembro de la población actuara como un halcón el 58,3% de las veces, y como una paloma el 41,7% de las veces. ¿Los humanos hacemos eso? Después de todo, amigos lectores, una lectura de Maquiavelo nunca viene mal. En este resultado, que recibe también el nombre de estrategia evolutivamente estable, la puntuación media de la población es de 6,25 puntos frente a los 15 puntos de una idílica población formada sólo por palomas. La situación estable no tiene por qué ser necesariamente el mejor de todos los mundos posibles; así que no se queje de la fauna que convive en su proyecto, hombre.