Pero este acto de procrastinación nunca es indefinido y se encuentra finalmente con un límite: el que marca el fatídico hito de control de gestión, por ejemplo. Concretamente el día antes de dicho evento es cuando el equipo de proyecto se dedica ha realizar el gran acto de memoria e intentar recordar cuántas horas dedicó a cada proyecto durante cada uno de los días del último mes, en el mejor de los casos; o cómo se distribuye el coste efectuado del mes en las diferentes partidas presupuestarias y/o tareas realizadas. Y cuando la memoria falla, otra característica bastante humana, vaya, es la de inventar.
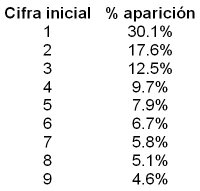
Pongámonos en el lugar del atribulado controller. ¿Hay alguna forma de comprobar si los datos son reales o inventados? Los falsificadores de datos deberían ponerse a temblar, ya que parece ser que cuando la gente inventa números que parezcan verosímiles tiende a utilizar más el 5 y el 6 como cifras iniciales –entenderemos por cifra inicial la primera cifra del número, leyendo de izquierda a derecha, que es diferente de cero. ¿Algún problema con ello? Podría utilizarse algún mecanismo para que la cifra inicial de nuestros números inventados se distribuyera aleatoriamente de una forma más uniforme. No hay motivos para que el falsificador deje de temblar. Todo indica que las series de números de cualquier documento contable honesto siguen la ley de Benford, teniendo como cifra inicial el 1 la mayoría de las veces y disminuyendo su frecuencia a medida que la cifra inicial es mayor, siendo el 9 el que menos veces se repite. En concreto, el porcentaje de aparición se muestra en la tabla siguiente:
Cómo haría entonces nuestro atribulado controller para detectar una acción fraudulenta? Utilizando una herramienta del tipo que encontrará en este sitio, para comprobar si la serie de datos que le han proporcionado sigue o no la ley de Benford. Desafortunadamente no constituye una prueba definitiva ya que el avispado falsificador podría haber amañado los datos de forma que sigan la ley de Benford. En todo caso sería una forma de desenmascarar falsificadores ignorantes de la ley de Benford. El primero en sugerir el uso de la ley de Benford para detectar irregularidades en contabilidad fue el contable y matemático Mark J. Nigrini, en un artículo publicado en 1996 en el nº 18 del Journal of the American Taxation Association, titulado “A Taxpayer Compliance Application of Benford's Law” –ver en este sitio un artículo más accesible. Desde entonces los auditores están al tanto de este hecho. ¿Lo está el del lector? ¿Lo estaban los de la antigua Andersen cuando auditaban a Enron?...
Para finalizar, un gráfico comparativo que muestra cómo cantan los datos del falsificador a pecho descubierto o del que simula de forma aleatoria.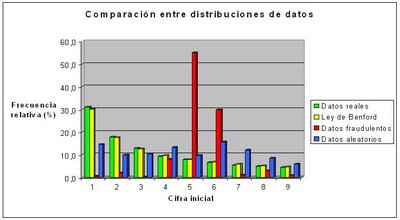
Me parece que tu grafico no es del todo correcto. Si generamos datos en forma "ALEATORIA", estos datos se caracterizan por tener la misma probabilidad de ocurrencia en sus digitos es decir que los primeros digitos por ejemplo el 1 y el 2 tendrian la misma probabilidad de ocurrencia que el 7 8 o 9, por lo que porcentualmente representarian entre un 9% al 11% de probabilidad.
ResponderEliminarSeria interesante que publiques un enlace o los datos con los cuales se generaron el grafico para hacer comprobaciones.
ResponderEliminarDaniel, gracias por tu puntualización. La verdad es que no recuerdo de donde saqué los datos del ejemplo, pero obviamente si la serie que se indica como datos aleatorios significa que se generaron de forma aleatoria cada uno de ellos, deberían haber salido porcentajes dentro del rango que tú indicas (por ejemplo 10,3 - 11,3 - 10,8 - 11,1 - 11,3 - 11,4 - 11,3 - 11,6 - 10,9), y no como muestra la figura. Otra cosa es que esa aleatoriedad se haya generado de otra manera diferente. Para evitar confusiones he cambiado el ejemplo teniendo en cuenta una "correcta" aleatoriedad. En este momento no me es posible corregir el gráfico, por lo que lo haré más tarde.
ResponderEliminar